Texto de: Marlliton Souza
Introdução
Conjuntos (ou sets) são estruturas de dados que armazenam uma coleção de valores únicos. Essa estrutura deriva dos conjuntos da matemática, e para entendê-la precisamos primeiro relembrar o que são conjuntos do ponto de vista matemático.
Na matemática, um conjunto é uma coleção de itens ou objetos distintos, sem uma ordem específica entre eles. Por exemplo, o conjunto dos números naturais consiste em números inteiros maiores ou iguais a zero, representado como N = {0, 1, 2, 3, 4, 5,...}.
Esse conjunto também pode ser representado da seguinte forma:

Você também pode imaginar que um conjunto seja um array sem elementos repetidos e sem o conceito de ordenação.
Por hora, isso é suficiente para começarmos a trazer esse conceito para computação, e a medida que formos avançando, abordaremos outros conceitos matemáticos conforme necessário.
Classe Set (nativa)
Poderíamos fazer nossa própria implementação de uma classe para representar um conjunto, mas como o JavaScript já possui uma classe Set nativa em sua API, usaremos essa classe para nossos exemplos.
A classe Set provê diversos métodos que podem ser muito úteis, alguns deles são:
add: adiciona um novo elemento no final do conjunto;size: retorna a quantidade de elementos do conjunto;clear: remove todos os elementos do conjunto;delete: remove o elemento especificado do conjunto;has: retorna um boolean caso o elemento especificado exista no conjunto ou não;values: retorna todos os valores presentes no conjunto.
Você pode conferir a lista completa de todos os métodos disponíveis clicando aqui. No entanto, é importante notar que alguns desses métodos podem não ser suportados por todos os navegadores. Portanto, antes de utilizá-los em um ambiente de produção, é recomendável verificar sua compatibilidade.
Neste artigo, optarei por não utilizar os métodos que não são suportados pelos navegadores, como o método union, que retorna a união de dois conjuntos. Como este método ainda não é suportado pelos navegadores até a data de publicação deste artigo, desenvolveremos nossa própria lógica para realizar as operações matemáticas necessárias.
Operações sobre conjuntos
Nesta seção, discutiremos alguns dos conceitos matemáticos sobre os conjuntos, depois traremos esse conceito para o contexto da programação.
União
A união entre conjuntos, é definida da seguinte forma: A ∪ B = {x | x ∈ A ou x ∈ B}, isso significa que a união será composta por elementos que genericamente chamaremos de x sendo que x pertence ao conjunto A ou x pertence ao conjunto B.
Graficamente, isso pode ser representado da seguinte forma:
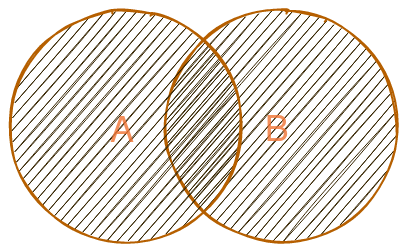
Para sabermos a união entre dois conjuntos usando a classe Set do JavaScript é bem simples, basta pegarmos os conjuntos A e B e espalharmos esses conjuntos num terceiro conjunto. Como os conjuntos no JavaScript não aceitam repetições, o resultado será a união dos dois conjuntos.
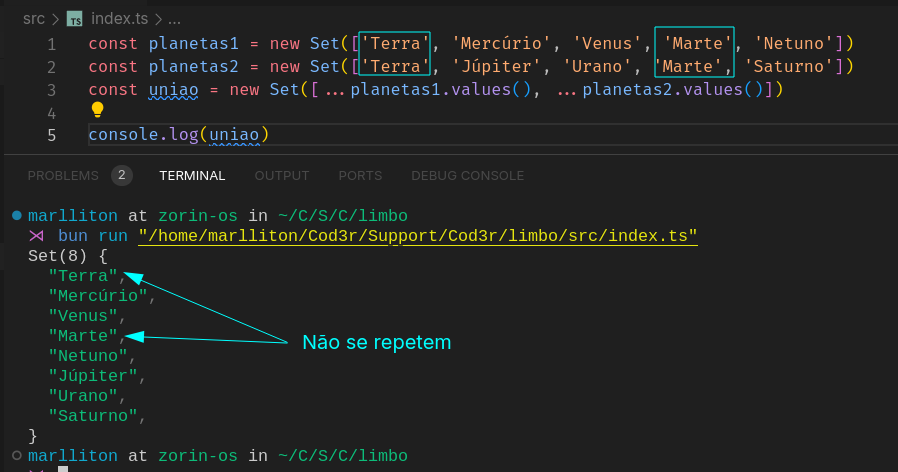
Perceba que apesar dos planetas, Terra e Marte estarem presentes em ambos os conjuntos, na união, eles só aparecem uma única vez.
Intersecção
A intersecção entre conjuntos é definida da seguinte forma: A∩B = {x | x ∈ A e x ∈ B}, isso significa que x pertence tanto ao conjunto A quanto ao conjunto B. Dessa forma, a intersecção pode ser entendida como os dados compartilhados entre os conjuntos.
Graficamente, isso pode ser representado da seguinte forma:
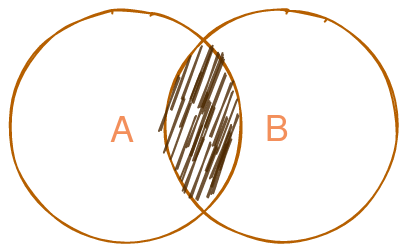
Para obtermos os elementos compartilhados entre os dois conjuntos, basta filtrarmos os elementos do conjunto A que estão presentes no conjunto B. E para saber se um elemento está contido em um conjunto podemos usar o método has.
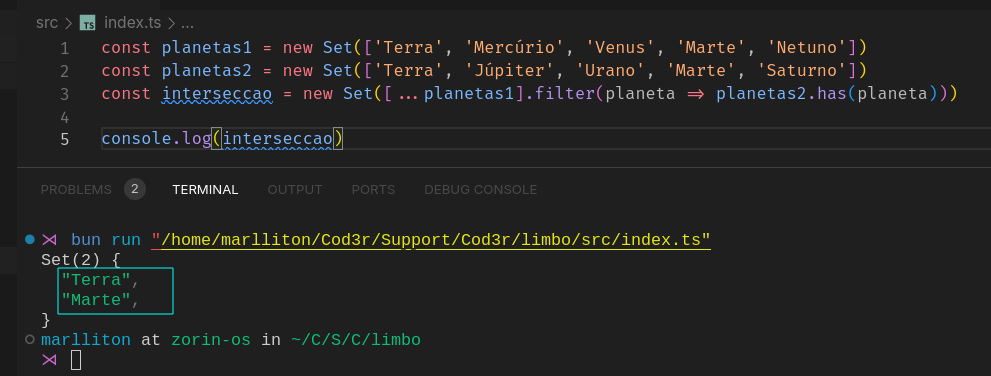
Então, ao executarmos o código acima, como esperado, o conjunto interseccao contém apenas os elementos Terra e Marte, pois esses são os únicos elementos compartilhados entre os dois conjuntos.
Diferença
A diferença entre conjuntos é definida da seguinte forma: A-B = {x | x ∈ A e x ∉ B}, isso significa que x pertence ao conjunto A, mas x não pertence ao conjunto B.
Graficamente, isso pode ser representado da seguinte forma:
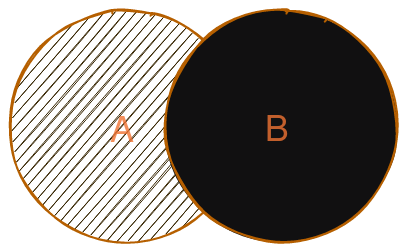
Para obtermos a diferença entre o conjunto A e B, basta filtrar os elementos que estão em A, mas não estão em B.
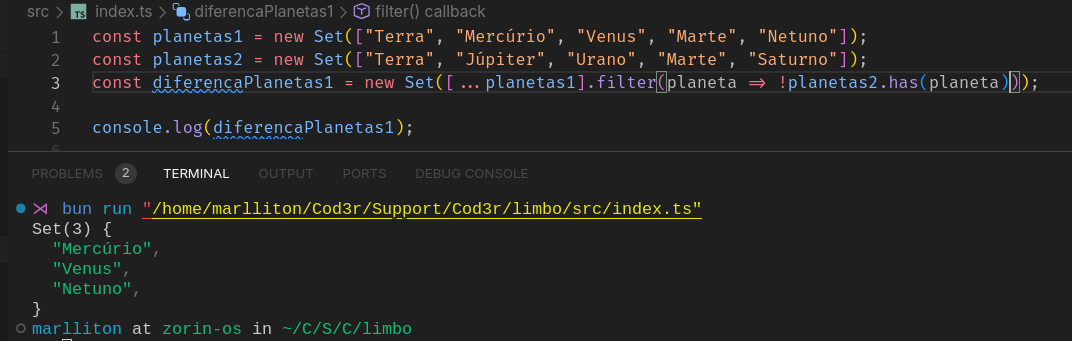
O resultado dessa operação é Mercúrio, Venus e Netuno, sendo os únicos elementos não presentes no conjunto planetas2.
Subconjuntos
Por último, falaremos sobre subconjuntos. Na matemática, pode ocorrer do conjunto A ser um subconjunto de B, o que é definido da seguinte forma:

Isso significa que para todo elemento x pertencente ao conjunto A, também deve pertencer ao conjunto B.
Graficamente, isso pode ser representado da seguinte forma:
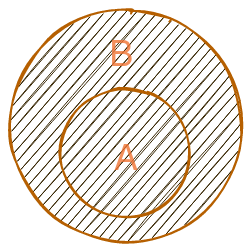
Dessa vez, queremos saber se o conjunto A é um subconjunto de B, então basta verificarmos se, todos os elementos de A estão presentes em B. Para isso, modificarei um pouco o conjunto planetas1 para que de fato ele seja um subconjunto de planetas2.
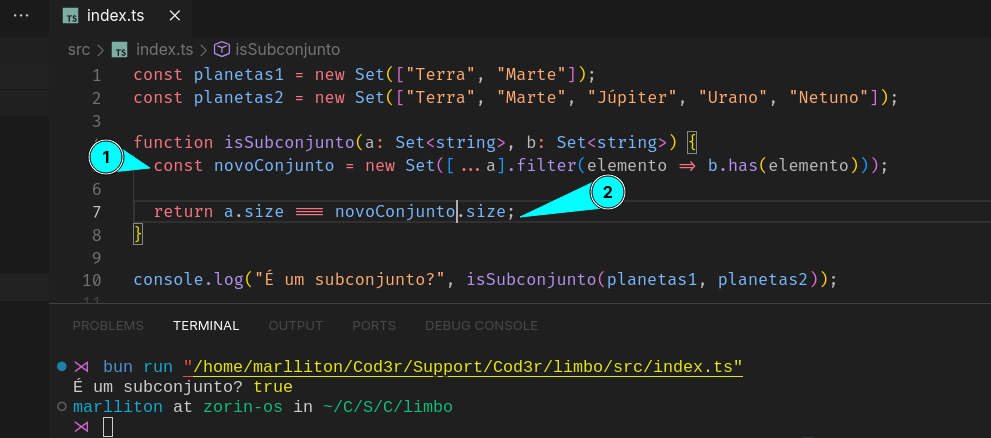
A lógica aqui é criar um terceiro conjunto (novoConjunto) para verificar se todos os elementos de A estão contidos em B.
No final, para saber se A é um subconjunto de B, basta verificar o novoConjunto tem o mesmo tamanho do conjunto A.
Conclusão
Os conjuntos são estruturas de dados muito úteis e neste artigo conhecemos um pouco da classe Set do JavaScript que pode ser usada para resolver problemas do dia a dia. Vale ressaltar que as operações matemáticas que fizemos aqui já se encontram nativamente dentro da classe Set, porém ainda não suportadas pela maioria dos navegadores e por isso desenvolvemos nossa própria lógica.
Conheça outras estruturas de dados
Pilhas (stacks): o que são, como funcionam e exemplos práticos

